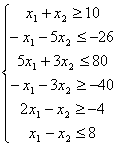
_{1. Графічним способом}

_{2. Симплекс методом.}

_{3. Розв'язавши двоїсту задачу}

_{Розв'язок}

 1.

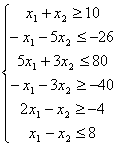
Розв’язок

Побудуємо множину допустимих розв'язків системи нерівностей

Заштрихована область на малюнку є множиною допустимих розв'язків. Червоним показано лінію рівня цільової функції а також вектор-градіент, який має координати (-45;-36). Так як нам потрібно мінімізувати функцію, то будемо рухати лінію рівня в напрямку антіградієнта до перетину з межею допустимої області. Як видно з малюнку це точка (10;10). Вона обведена колом. Таким чином

Для розв’язку задачі симплекс методом запишемо умову задачі в канонічній формі задачі лінійного програмування

Будуємо симплекс таблицю. Як бачимо, розв’язок не допустимий, тому вводимо вільну змінну  в базисні

Розв’язок знову не допустимий. Вводимо змінну  у базисні

Розв’язок допустимий, але не оптимальний, тому робимо ще один крок.

Розв’язок знову не оптимальний, тому робимо ще один крок

Тепер розв’язок є оптимальним. Розв’язок прямої задачі ,

Сформулюємо двоїсту задачу. Для цього приведемо всі нерівності до вигляду

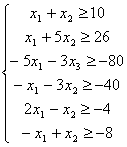
Тепер можемо сформулювати двоїсту задачу

Відповідність між змінними прямої та двоїстою задачі:

Складаємо симплекс таблицю

Бачимо, що розв’язок не допустимий, тому робимо ще один крок

Розв’язок двоїстою задачі . Оптимальне значення цільової функції

Зауважимо, що рядок коефіцієнтів цільової функції прямої задачі відповідає вільним змінним двоїстої задачі і навпаки. Крім того, максимум цільової функції двоїстою задачі співпадає з мінімумом цільової функції прямої задачі