Примеры --- Линейное программирование --- Алгоритмы отсечения
Одним із методів відтинання розв'язати задачу цілочислового програмування:
, 
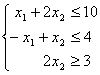Розв'язок
Розв'яжемо спочатку ЗЛП сімплек-методом без обмежень на цілочисленність змінних
Канонічний вид ЗЛП
Будуємо сімплекс-таблицю
|
|
Св |
Х1 |
Х2 |
|
Х3 |
10 7 |
1 1 |
2 1 |
|
Х4 |
4 2.5 |
-1 -1 |
1 0.5 |
|
Х5 |
-3 1.5 |
0 0 |
-2 -0.5 |
|
-L |
0 -4.5 |
-1 -1 |
3 1.5 |
|
|
Св |
Х1 |
Х5 |
|
Х3 |
7 2 |
1 3 |
1 -2 |
|
Х4 |
2.5 5 |
-1 -2 |
0.5 2 |
|
Х2 |
-1.5 4 |
0 -1 |
-0.5 1 |
|
-L |
-4.5 -12 |
-1 2 |
1.5 -3 |
|
|
Св |
Х1 |
Х5 |
|
Х3 |
2
|
3
|
-2
|
|
Х4 |
5
|
-2
|
2
|
|
Х2 |
4
|
-1
|
1
|
|
-L |
-12
|
2
|
-3
|
Отримане
рішення є оптимальним для ЗЛП, але недопустимим для ЗЦЛП, оскільки є
нецілочисленні змінні. Побудуємо відтинання для змінної 
, використовуючи перший
алгоритм Гоморі
|
|
Св |
Х3 |
Х5 |
|
Х1 |
2 |
1 |
-2 |
|
Х4 |
5 |
0 |
2 |
|
Х2 |
4 |
0 |
1 |
|
Х6 |
2 |
1 |
-3 |
|
-L |
-10 |
1 |
-5 |
Проаналізувавши строку цільової функціі бачимо, що розв'язок допустимий, але неоптимальний, тому робимо це один крок
|
|
Св |
Х3 |
Х6 |
|
Х1 |
2 2 |
1 1 |
-2 2 |
|
Х4 |
5 5 |
0 0 |
2 2 |
|
Х2 |
4 4 |
0 0 |
1 1 |
|
Х5 |
2 0 |
1 -1 |
-3 -1 |
|
-L |
-10 -12 |
1 -1 |
-5 -3 |
Тепер
строка цільової функції від'ємна, отже розв'язок оптимальний 
Відповідь:
