Примеры --- Решение задач из задачника Филиппова -- 448

№448

Сделаем замену , тогда , . Исходное уравнение примет вид

Сделаем замену , тогда . Уравнение принимает вид

1)

2)

Имеем уравнение, не разрешенное относительно производной.

Найдем полный дифференциал от обеих частей уравнения

Учитывая, что , получим

Окончательное решение в параметрическом виде

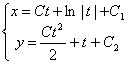
Для получения ответа в форме, записанной в ответах, достаточно положить , 

Мы решали уравнение, не разрешенное относительно производной. Проверим, существует ли особое решение.

Дифференцируем уравнение  по

.

Ответ: 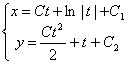,  ,