№ 268

№ 268

Вводим параметр

Исходное уравнение тогда запишется в виде

Поскольку не являются решениями (в чем легко убедится, подставив в исходное уравнение), делим обе части на :

Берем полный дифференциал от обеих частей равенства

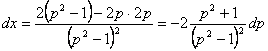
Учитывая, что , получим

Таким образом, решение уравнения в параметрическом виде

Исследуем, есть ли у уравнения особые решения.

Дифференцируем обе части исходного уравнения по

Откуда

Подставляем это значение в исходное уравнение:

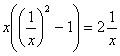
Решений нет, следовательно особых решений уравнение не имеет

Ответ: